![[번역] 부동 소수점 문제의 예시 (Examples of floating point problems)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FCGRTf%2FbtrW2t4ZW6W%2FAAAAAAAAAAAAAAAAAAAAAIfLQS-E4LFhSfCEzDlibBzgPTSURTiLH_hLpAZSNL5P%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DxgZODW4Q7xYm4FLdJ8Vw1NEs9kk%253D)

지인이 부동 소수점(Floating Point)과 관련한 글을 가져와 흥미롭게 읽어보다가, 한국어로 번역된 자료가 있었으면 하는 바람으로 원본 작성자 분께 허락을 구하여 번역본을 게시합니다. 문장 생략 및 추가 등 의역이 일부 포함되어 있는 점 참고 바랍니다.
원문은 아래의 링크에서 보실 수 있습니다.
Examples of floating point problems
Hello! I’ve been thinking about writing a zine about how things are represented on computers in bytes, so I was thinking about floating point. I’ve heard a million times about the dangers of floating point arithmetic, like: addition isn’t associative
jvns.ca
※ 본 글의 한국어 번역 게시를 허락해 주신 Julia Evans님께 감사의 말씀을 전합니다.
안녕하세요! 저는 컴퓨터에서 데이터가 바이트로 표현되는 방식에 대한 글을 써보려고 합니다. 그중 이번에는 부동 소수점(floating point)에 대한 이야기를 해볼까 합니다.
저는 부동 소수점 사용의 위험성에 대해 수도 없이 들어왔습니다, 예를 들어
|
하지만 이러한 문제들이 그 자체로는 조금 추상적으로 느껴졌고, 실제 프로그램에서 부동 소수점 문제가 발생한 구체적인 사례가 궁금했습니다.
그래서 Mastodon에서 사람들에게 실제 프로그램에서 겪은 부동 소수점 문제를 물어봤고, 여러 예시를 받을 수 있었습니다. 아래에는 여러 가지 예시와 함께 일부 문제를 직접 확인하기 위한 예제 프로그램을 포함합니다. 목차는 다음과 같습니다:
|
위의 예시에는 NaN 또는 +0/-0, 무한대 값, 서브노멀 값은 다루지 않습니다. 이들이 문제를 일으키지 않는 것은 아니지만, 쓰다 보니 지쳐서 더 이상 쓰지 못했습니다.
부동 소수점(Floating Point)은 어떻게 작동하는가?
이 글에서는 부동 소수점이 어떻게 작동하는지에 대해서는 길게 설명하지는 않을 예정입니다. 대신 제가 몇 년 전에 작성한 일러스트에서 부동 소수점의 기본 개념을 다루고 있으니 참고해 주세요.

부동 소수점은 '나쁘거나' 랜덤하지 않다
저는 당신이 이 글을 읽고 '부동 소수점은 나쁘다(bad)'는 결론을 내리지 않길 바랍니다. 부동 소수점은 숫자를 계산하는 데에 있어 엄청난 도구입니다. 수많은 똑똑한 사람들은 컴퓨터에서 숫자 계산을 효율적이고 정확하게 하기 위해 많은 노력을 기울여 왔습니다. 다음 두 가지는 부동 소수점의 잘못이 아니라는 점을 분명히 말씀드리고 싶습니다:
여러분이 이 글을 읽고 부동 소수점이 무작정 '나쁘다'라는 결론을 내리지 않았으면 좋겠습니다. 부동 소수점은 수치 계산을 수행하기 위한 엄청난 도구입니다. 컴퓨터에서 수치 계산을 효율적이고 정확하게 하기 위해 수많은 사람들이 많은 노력을 기울여 왔습니다. 부동 소수점 자체가 문제가 아니라는 점을 보여주는 두 가지를 설명드릴게요:
- 컴퓨터로 수치 연산을 할 때는 본질적으로 어느 정도의 근사치(근접값)와 반올림이 수반되며, 특히 효율적으로 계산하기 위해서는 더더욱 그렇습니다. 연산하는 모든 숫자에 대해 임의의 정밀한 값을 보장할 수 없습니다.
- 부동 소수점은 표준화(IEEE 754)되어 있으므로 부동 소수점 덧셈과 같은 연산은 결정론적(deterministic)입니다 – 제가 알기로는 0.1+0.2는 다른 아키텍처에서도 항상 '정확히' 같은 결과인 0.30000000000000004를 얻을 수 있습니다. 예상한 값이 아닐 수도 있지만, 사실 매우 예측 가능한 결과입니다.
이 글의 목표는 부동 소수점 숫자에서 발생할 수 있는 문제와 그 이유를 설명함으로써, 언제 조심해야 하고 언제 부적절한 상황이 발생하는지 아는 데에 도움을 드리는 것입니다.
이제부터 예제를 살펴보겠습니다.
Example 1 - 멈춰버린 주행 거리계(odometer)
어떤 사람이 32비트 부동 소수점 숫자를 사용하여 이동 거리를 측정하는 주행 거리계(Odometer)를 작업하고 있었는데, 작은 값을 계속 더하다가 큰 문제가 발생했다고 합니다. 구체적으로 설명하자면, 주행 거리계에 한 번에 1cm씩 계속 늘려가며 측정한다고 가정해 봅시다. 그렇다면 10,000km, 즉 1,000,000,000cm만큼 움직였다고 하면 어떤 일이 벌어질까요?
아래는 이를 구현한 C언어 프로그램입니다.
#include <stdio.h>
int main() {
float meters = 0;
int iterations = 100000000;
for (int i = 0; i < iterations; i++) {
meters += 0.01;
}
printf("기대 값: %f km\n", 0.01 * iterations / 1000 );
printf("실제 값: %f km \n", meters / 1000);
}
이에 대한 출력값은 이렇게 나오네요.
Expected: 10000.000000 km
Got: 262.144012 km
이건 뭔가 확실히 잘못됐습니다. 작은 오차가 아니라, 262km는 10,000km와 비교하면 엄청나게 작은 거리예요. 도대체 무슨 일이 일어난 걸까요?
무엇이 잘못됐는가: 부동 소수점 숫자 간의 간격
이 사례에서의 문제는 32비트 부동 소수점 숫자를 사용할 때, 262144.0+0.01의 결과는 262144.0라는 결과가 나온다는 점입니다. 즉, 숫자가 부정확할 뿐만 아니라 실제로도 전혀 증가하지 않게 되는 겁니다. 위의 예시에서 10,000km를 더 이동한다고 해도 주행계에는 여전히 262,144m(= 262.144km)에 머물러 있습니다.
왜 이런 일이 생길까요? 부동 소수점 숫자 사이의 간격은 값이 커질수록 더 커지기 때문입니다. 연속된 3개의 32비트 부동 소수점 숫자를 가져와보겠습니다.
- 262144.0
- 262144.03125
- 262144.0625
이 번호는 float.exposed에서 '유효숫자(significand)'를 몇 번 증가시켜 얻은 값들입니다. 위 세 숫자는 연속된 숫자입니다. 즉, 262144.0과 262144.03125 사이에는 32비트 부동 소수점 숫자가 없다는 겁니다. 이게 왜 문제일까요?
문제는 262144.03125가 약 262144.0+0.03이라는 점입니다. 따라서 262144.0에 0.01을 더하려고 할 때 다음 숫자로 반올림하는 것이 불가능합니다. 따라서 합은 여전히 262144.0에 머무르게 되는 겁니다.
그리고 여기서 262,144는 2의 거듭제곱(2^18)인 것도 우연이 아닙니다. 부동 소수점 숫자의 간격은 매번 2의 거듭제곱에 따라 달라지며, 2^18에서 32비트 부동 소수점 숫자 사이의 간격은 0.016에서 0.03125로 증가합니다.
이 문제를 해결하는 한 가지 방법: double 사용하기
64비트 부동 소수점을 사용하면 이 문제가 해결됩니다. 위의 C 프로그램에서 float 대신 double을 사용하면 결과가 훨씬 더 정확해지고, 우리가 의도한 대로 프로그램도 작동하게 됩니다. 출력은 다음과 같습니다:
기대 값: 10000.000000 km
실제 값: 9999.999825 km
여전히 약간의 부정확성은 남아있지만, 이는 약 17cm 정도의 작은 오차입니다. 이런 오차가 중요한가는 상황에 따라 달라집니다. 예를 들어 정밀한 계산이 필요한 우주 비행에서는 약간의 오차도 큰 문제가 될 수 있겠지만, 앞서 다룬 예제의 주행 거리계라면 크게 문제가 되지는 않을 겁니다.
또 다른 개선 방법은 더 큰 단위로 주행 거리계의 값을 갱신하는 겁니다. 예를 들어 1cm씩 주행 거리를 늘리는 대신, 50cm마다 업데이트하는 방식으로 빈도를 줄일 수 있습니다.
double을 사용하고 1cm 대신 50cm씩 더한다면, 조금 더 정확한 결과를 얻을 수 있습니다. 코드를 따로 제공하지는 않겠지만, 이에 따른 결과는 다음과 같습니다:
기대 값: 10000.000000 km
실제 값: 10000.000000 km
또 다른 해결 방법: 정수 사용하기
세 번째 해결 방법은 정수(integer)를 사용하는 방법이 있습니다: 예를 들어 우리가 신경 쓰는 단위를 0.1mm로 정하고, 모든 값을 0.1mm의 정수 배(interger multiple)로 측정하는 것입니다. 다만, 저는 주행 거리계를 만들어본 적이 없어서 어떤 방법이 최선이다라고 확실하게 말씀드리기는 어렵네요.
Example 2 - Javascript에서 Tweet ID
Javascript는 부동 소수점 숫자만 지원하며, 정수형 타입이 따로 없습니다. 64비트 부동 소수점 숫자로 표현할 수 있는 가장 큰 정수는 2^53입니다.
하지만 Tweet(트윗) ID는 2^53보다 훨씬 큰 숫자입니다. 그래서 Twitter API는 현재 트윗 ID를 정수형과 문자열(String) 형태로 모두 반환합니다. Javascript에서는 문자열 ID(E.g., " 1612850010110005250")를 사용하면 되지만, 정수형 버전을 사용하려고 하면 문제가 발생합니다.
직접 확인해보고 싶다면 Tweet ID를 Javascript Console에 직접 입력해 보세요. 예를 들면 아래 사진처럼 말이지요.
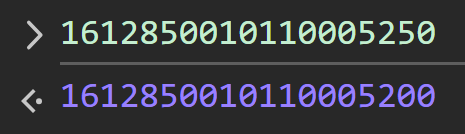
보시다시피, 1612850010110005200은 원래 숫자인 1612850010110005250과 같지 않습니다! 50이나 적은 숫자라고요.
이와 같은 문제는 Python이나 최소한 제가 아는 다른 언어들에서는 발생하지 않습니다. Python은 정수형 타입을 지원하기 때문입니다. 동일한 숫자를 Python Repl에 입력하면 다음과 같은 결과를 얻을 수 있습니다.
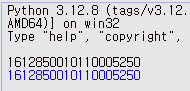
Python에서는 예상대로 정확한 숫자가 반환되는 모습을 볼 수 있습니다.
Example 2.1 - 손상된 JSON 데이터
이 문제는 앞서 다룬 'Javascript에서 Tweet ID' 문제의 변형에 해당합니다. Javascript 코드를 직접 작성하지 않더라도, JSON 데이터에 포함된 숫자가 종종 부동 소수점으로 처리될 수 있기 때문입니다. JSON의 이름에 'Javascript'가 포함되어 있기에, Javascript 방식으로 값을 디코딩하는 게 합리적으로 보일 수 있습니다.
예를 들어, JSON 데이터를 `jq`를 통해 처리하면 동일한 문제가 발생합니다.
$ echo '{"id": 1612850010110005250}' | jq '.'
{
"id": 1612850010110005200
}하지만 이 문제가 모든 JSON 라이브러리에서 발생하는 건 아닙니다. Python의 `json` 모듈은 1612850010110005250을 올바른 정수로 디코딩합니다.
또한, 몇몇 분들에 따르면 JSON으로 부동 소수점 값을 전송할 때 발생한 문제를 언급해 주셨습니다. 예를 들어, JSON으로 큰 정수(예: 포인터 주소)를 전송했을 때 데이터가 손상되거나, 작은 부동 소수점 값을 반복적으로 주고받는 동안 점진적으로 값이 틀어지는 현상이 발생했다고 합니다.
Example 3 - 잘못된 분산(Variance) 계산
통계를 계산한다고 가정해 봅시다. 많은 숫자의 분산을 계산하고자 하지만, 모든 숫자를 메모리에 담기 어려울 정도로 많기에 단일 패스(single pass)로 계산해 보겠습니다.
단일 패스로 분산을 계산할 수 있는 간단한, 하지만 매우 잘못된 알고리즘이 있습니다. 이는 한 블로그 포스트에서 소개된 방법입니다. 아래는 해당 알고리즘으로 구현한 Python 코드입니다:
import numpy as np
def calculate_bad_variance(nums):
sum_of_squares = 0
sum_of_nums = 0
N = len(nums)
for num in nums:
sum_of_squares += num**2
sum_of_nums += num
mean = sum_of_nums / N
variance = (sum_of_squares - N * mean**2) / N
print(f"Real variance: {np.var(nums)}")
print(f"Bad variance: {variance}")
우선, 이 잘못된 알고리즘으로 작은 숫자 5개의 분산을 계산해 봅시다. 결과가 꽤 괜찮아 보이네요:

이번에는 100,000개의 매우 큰 숫자를 사용해 봅시다. 이 숫자들은 서로 매우 가까운 값들로 되어있으며, 100,000,000에서 100,000,000.06 사이에 분포합니다.

이 결과는 정말 너무나 심각합니다. 잘못된 알고리즘이 계산한 분산이 아예 완전히 틀렸을 뿐만 아니라, 음수 값이 나왔습니다! (분산은 절대로 음수가 될 수 없으며 항상 0 이상이어야 합니다.)
무엇이 문제였을까: 치명적인 소실 (Catastrophic Cancellation)
여기서 발생한 문제는 주행 거리계(Odometer) 문제와 유사합니다. `sum_of_squares` 값이 매우 커지는데(약 10^21 또는 2^69), 이 시점에서 부동 소수점 숫자 사이의 간격도 2^46으로 매우 커집니다. 이로 인해 계산에서 모든 정밀도를 잃게 됩니다.
이 문제를 흔히 '치명적 소실 (Catastrophic Cancellation)'이라 합니다. 매우 큰 부동 소수점 숫자 두 개를 빼는 과정에서, 이 두 숫자 모두 계산의 올바른 값에서 크게 벗어난 상태이므로 뺄셈의 결과 또한 잘못된 값을 반환하게 됩니다.
앞서 언급한 블로그 글에서는 분산을 계산할 때 사람들이 사용하는 더 나은 알고리즘인 Welford 알고리즘을 소개합니다. 이 알고리즘은 치명적 소실 문제를 피할 수 있게 합니다. 그리고 대부분의 사람들이 쓸 수 있는 가장 간단한 해결책은 직접 분산을 계산하거나, 계산하는 함수를 작성하기보다는 Numpy와 같은 계산 라이브러리를 사용하는 것이 있습니다.
Example 4 - 언어마다 다른 부동 소수점 계산
여러 사람들이 서로 다른 플랫폼에서 동일한 계산 과정이 다르게 수행된다고 언급해 주셨습니다. 실무에서 이런 일이 발생하는 한 가지 예는, 프론트엔드 코드와 백엔드 코드에서 완전히 동일한 부동소수점 계산을 수행한다고 해도, Javascript와 PHP에서 각각 다르게 처리되어 사용자가 불일치한 결과를 보게 되고 혼란스러워하는 경우가 있겠네요.
원칙적으로 부동 소수점 연산은 IEEE 754 표준에 의해 정의되고 수행되므로, 항상 동일하게 동작해야 한다고 생각할 수 있습니다. 하지만 몇 가지 주의사항이 있습니다:
- `libc`에서의 수학 연산(예: sin, cos)은 구현마다 다르게 동작할 수 있습니다. 때문에 `glibc`를 사용하는 코드와 `musl`을 사용하는 코드는 다른 결과를 반환할 수도 있습니다.
- 일부 x86 명령어는 내부적으로 64비트 정밀도(precision) 대신 80비트 정밀도를 사용하여 몇몇 double 연산을 수행할 수 있습니다. 이와 관련한 Github Issue도 있습니다.
위 내용에 대해서는 확신이 없고, 제가 구현이 가능한 구체적인 예제를 가지고 있지는 않습니다.
Example 5 - Deep Space Kraken
Kerbal Space Program이라는 우주 시뮬레이션 게임에서, 과거에 "딥 스페이스 크라켄 (Deep Space Kraken)"이라는 버그가 있었습니다. 이 버그는 우주선이 매우 빠르게 움직일 때, 부동 소수점 문제로 인해 우주선이 파괴되는 현상이었습니다. 이는 앞서 이야기했던 큰 부동 소수점과 관련된 문제들, 예를 들어 잘못된 분산 계산과 같은 오류와 비슷하지만, 다음과 같은 이유로 따로 언급하고 싶었습니다.
- 이름이 재미있습니다 (It has a funny name)
- 이와 비슷한 오류가 비디오 게임, 천체물리학, 시뮬레이션 전반에서 매우 흔한 버그로 보입니다. 특히 원점에서 매우 멀리 떨어진 점(point)을 다룰 때, 수학적 계산이 엉망이 되는 경우가 많습니다.
비슷한 사례로는 마인크래프트(Minecraft)의 "Far Lands" 현상이 있습니다.
Example 6 - 부정확한 타임스탬프
이번이 마지막으로 다루는 "아주 큰 부동 소수점 숫자가 문제를 일으키는" 예제입니다. 하지만! 한 가지 더 이야기를 해보겠습니다.
현재의 Unix epoch 시간을 나노초 단위(약 1673580409000000000)로 표현한다고 상상해 봅시다. 이를 64비트 부동소수점 숫자로 저장하려고 한다면 어떻게 될까요?
결론부터 말하면, 이 방식은 적합하지 않습니다! 1673580409000000000은 대략 2^60에 해당하며, 2^53보다 큽니다. 따라서 이 값 바로 다음의 64비트 부동 소수점 숫자는 1673580409000000256입니다.
이로 인해 시간 계산에서 부정확성이 생길 수 있습니다. 다행히 시간 라이브러리는 일반적으로 시간을 정수로 표현하기 때문에 이런 문제는 보통 발생하지 않습니다. (물론, 2038년 문제가 남아 있긴 하지만, 이는 부동소수점과는 관련이 없습니다.)
이 예제가 주는 교훈은 때로는 정수를 사용하는 것이 더 나을 때도 있다는 것입니다.
Example 7 - 페이지를 열(column)로 나누기
지금까지 큰 부동 소수점 숫자와 관련된 문제를 살펴봤으니, 이번에는 작은 부동 소수점 숫자에서 발생하는 문제를 살펴보려고 합니다.
페이지의 너비(page width)와 열의 너비(column width)가 있다고 가정해 봅시다. 다음 두 가지를 계산하려고 합니다.:
- 페이지에 몇 개의 열이 들어갈 수 있는가 (How many columns fit on the page)
- 남은 공간, 즉 나머지가 얼마나 되는지 (How much space is left over)
이 계산을 할 때는 다음과 같이 하는 게 합리적일 거라 생각합니다.
- 첫 번째 질문: floor(page_width / column/width)
- 두 번째 질문: page_width % column_width
정수로는 위 방법이 잘 동작하지만, 부동 소수점에서는 문제가 생깁니다.
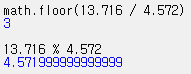
아래의 결과는 틀렸습니다. 13.716을 4.572로 나눈 나머지는 0이 되어야 하지만, 그렇지 않게 나옵니다.
남는 공간을 계산하는 더 나은 방법을 생각해 보자면, 13.716 - 3 * 4.572가 있을 겁니다. 이렇게 하면 매우 작은 음수가 나오긴 하지만 더 정확한 계산 결과에 가깝습니다.
이 예제에서 우리가 알 수 있는 점은 부동 소수점을 사용하여 계산을 할 때 동일한 값을 두 가지 다른 방식으로 계산하지 말라는 것입니다. 이는 매우 기본적인 예제이지만, 부동 소수점 숫자로 페이지 레이아웃을 설계하거나 CAD 도면 작업을 할 때 이런 문제가 다양한 형태로 발생할 수 있다는 점을 생각해 볼 수 있습니다.
Example 8 - 충돌 검사 (Collision Checking)
다음은 아주 간단한 Python 프로그램입니다. 이 프로그램은 변수 a가 1,000에서 시작해서 0에 충돌할 때까지 계속 감소시킵니다. 예를 들어 퐁(Pong) 같은 게임에서 공이 벽에 충돌하는 상황을 시뮬레이션한다고 생각해볼 수 있겠네요.
a = 1000
while a != 0:
a -= 0.001
print(a)이 프로그램이 정상적으로 실행되고 종료될 것이라 기대할 수 있습니다. 하지만 실제로는 그렇지 않습니다. (실제로 실행할 때는 1000이 아닌 작은 수로 정해도 됩니다)

a는 절대로 정확히 0이 되지 않습니다. 대신 a는 다음 값들 사이를 오가게 됩니다: 1.673494676862619e-08 ~ -0.0009999832650532314
여기서 우리가 얻을 있는 교훈은 부동 소수점 값을 비교할 때 '정확히 같은지 (equality)'를 검사할 필요가 없다는 겁니다. 대신 두 숫자가 매우 작은 오차 안에서 다른지 여부를 확인하는 것이 좋습니다. 위의 경우라면 a != 0 대신에 a > 0와 같이 쓸 수 있습니다.
여기까지입니다
NaN, 무한대 값, +0/-0, 서브노멀에 대해서는 다루지 못했지만, 이미 충분히 많은 글을 썼으니 여기서 말을 줄이려 합니다. 나중에 후속 포스트를 작성할지는 모르겠네요. Mastodon에서의 스레드만 해도 부동소수점 문제에 대해 15,000자나 되는 자료가 있으니까요. 다룰 내용이 정말 많습니다! 아니면, 글을 안 쓸 수도 있겠죠. 누가 알겠나요 :)
※ 본 글의 한국어 번역 게시를 허락해 주신 Julia Evans님께 감사의 말씀을 전합니다.
'[ IT ] > Develop' 카테고리의 다른 글
| Linux 환경에서 USB 프린터를 네트워크 공유하기 (0) | 2025.08.14 |
|---|---|
| Android용 SMS/MMS Extractor (문자 추출 앱) (335) | 2024.07.08 |
| 안드로이드용 트위터 인용 보기 (442) | 2024.01.13 |
| 네이버 치지직(CHZZK) API [작성 중] (338) | 2023.12.22 |

개발 적당히, 정치 적당히, 일상 적당히, 그냥 뭐든지 적당히만 하는 소프트웨어전공 대학생, 쏘가리입니다. / Profile Image by REN (Twitter @Ren_S2_)


